|
|
||||
|
||||
|
|
I can do just what I wish [in my research] ... The king calls me his professor, and I think I am the happiest man in the world.
Leonhard Euler
Current active fields of research are
- Percolation
- Stable Matchings
- Lattice Animals
- Random Number Generation
- Computational Complexity and Statistical Mechanics
- Low autocorrelated binary sequences
Percolation

Percolation (from Latin percolare, "to filter" or "trickle through") refers to the movement and filtering of fluids through porous materials. In percolation theory, the porous material is modeled as a lattice or graph, on which the open pores are randomly selected vertices or edges at a given density. Percolation models are the simplest models in statistical physics that have a phase transition with universal critical exponents. My research on percolation so far focussed on numerical and rigorous results on the cluster-density, i.e. the average number of connected clusters of pores per lattice site and on computing precise numerical values for the percolation threshold in hyperbolic lattices.
Click here to learn more, read the papers or download the data.
Stable Matchings
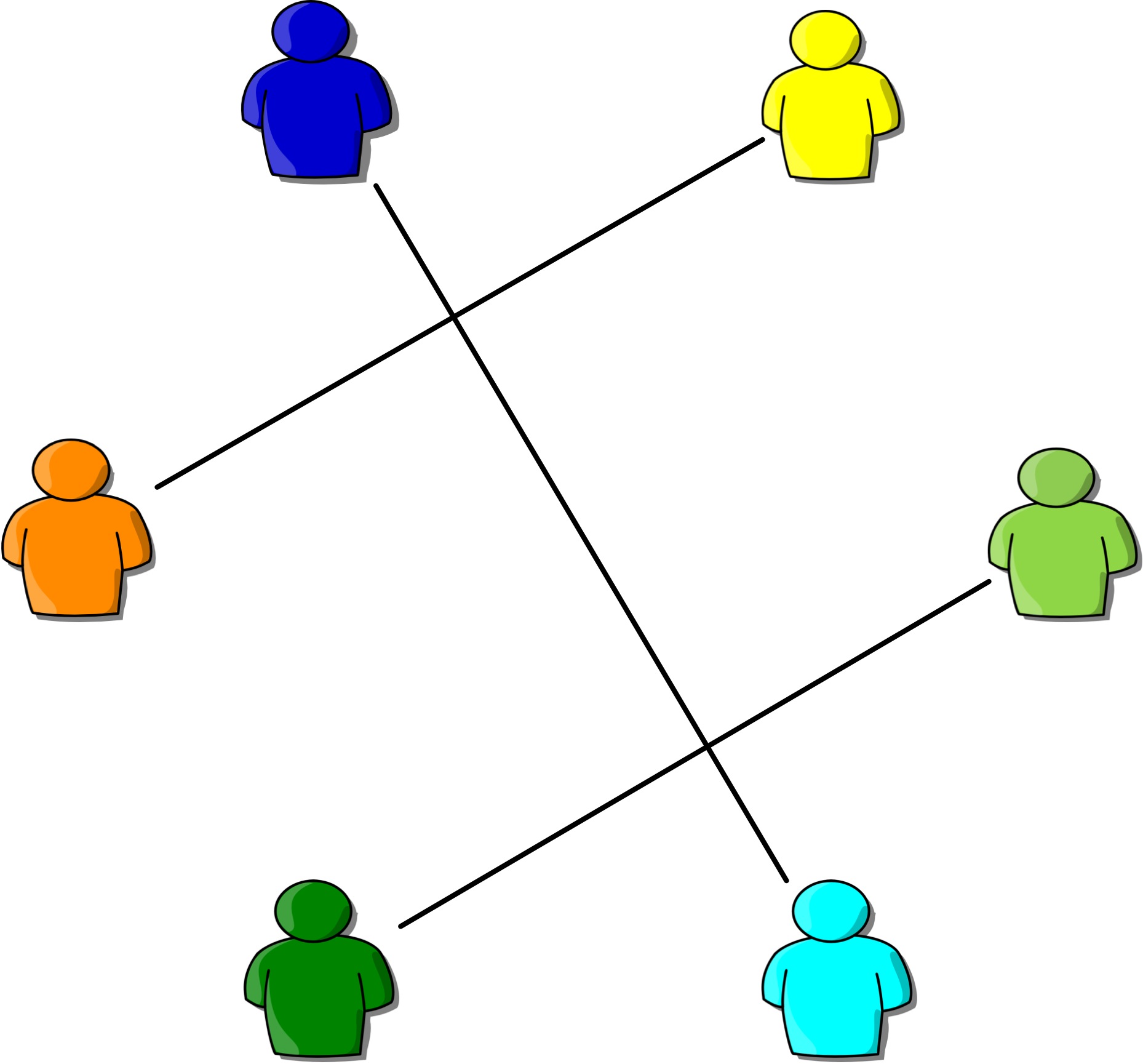
The stable matching problem is a prototype model in economics and social sciences where agents act selfishly to optimize their own satisfaction, subject to mutually conflicting constraints. A paradigmatic example is the stable roommates problem. Consider an even number n of participants. Each of the participants ranks all the others in strict order of preference. A matching is a set of n/2 disjoint pairs of participants. A matching is stable if there is no pair of unmatched participants who both prefer each other to their partner in the matching. Such a pair is said to block the matching. The stable roommates problem is to find a stable matching. The name originates from the problem to assign students to the double bedroomes of a dormitory. Another application is the formation of cockpit crews from a pool of pilots.
It is well known that not all instances of the stable roommates problem admit a solution. My research focuses on computing the probability pn that a random instance with n participants admits a solution. For that I developped a sublinear algorithm to solve large random instances of the stable roommates problem. I also used a computer algebra system to compute pn exactly for small instances.
Click here to learn more, read the papers or download the data.
Lattice Animals
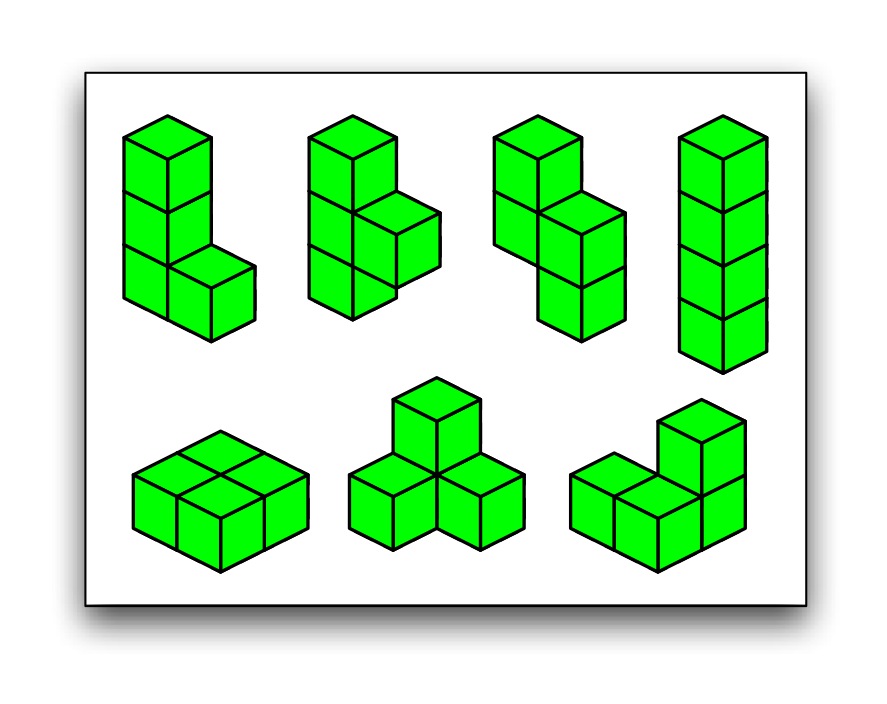 A lattice animal is a finite set of connected vertices of a regular lattice. Lattice animals on the square lattice are better known
as polyominoes. On the cubic lattice they are called
polycubes. The figure on the left shows all polycubes of size n = 4.
A lattice animal is a finite set of connected vertices of a regular lattice. Lattice animals on the square lattice are better known
as polyominoes. On the cubic lattice they are called
polycubes. The figure on the left shows all polycubes of size n = 4.
The enumeration of lattice animals is a longstanding combinatorial problem that has some motivations in physics, for example in the study of branched polymers and percolation. For most lattices we don't know a formula for the number of lattice animals of a given size n, and all we can do is to count them one by one. Since the number of lattice animals grows exponentially with n, this counting is a demanding task, even with a fast computer.
We develop fast algorithms for the enumeration of lattice animals and we run these algorithms on parallel computers. We also work on combinatorial arguments that complement computer based enumerations.
Click here to learn more, read the papers or download the data.
Random Number Generation
 A computer can do almost everything with numbers - except generating them
randomly. As a
deterministic machine, the computer is incapable of producing any sort of randomness.
Yet a decent fraction of CPU cycles consumed worldwide is devoted to the
generation of
pseudo random numbers, especially in computational
physics. The term “pseudo” refers to the fact that these numbers are
generated by a deterministic algorithm a.k.a.
random number
generator. The generator should produce a sequence of numbers that
cannot be distinguished from a sequence of “truly” random numbers,
not distinguished by any measurements on finite parts of the sequence.
The insanity of this idea is so obvious
that it is a miracle why it actually works.
A computer can do almost everything with numbers - except generating them
randomly. As a
deterministic machine, the computer is incapable of producing any sort of randomness.
Yet a decent fraction of CPU cycles consumed worldwide is devoted to the
generation of
pseudo random numbers, especially in computational
physics. The term “pseudo” refers to the fact that these numbers are
generated by a deterministic algorithm a.k.a.
random number
generator. The generator should produce a sequence of numbers that
cannot be distinguished from a sequence of “truly” random numbers,
not distinguished by any measurements on finite parts of the sequence.
The insanity of this idea is so obvious
that it is a miracle why it actually works.
Well, sometimes it doesn't work. Every now and then a well designed, well tested and well established random number generator fails to fake randomness in a simulation. A famous example is the Ferrenberg affair. Since a well designed and well tested random number generator has no obvious flaws, explaining the failure requires a forensic investigation. It took more than 10 years and various attempts before the Ferrenberg affair could finally be settled.
The theoretical background of the Ferrenberg affair was Heiko Bauke's and mine first contribution to the field. A second paper demonstrates the bias in some popular random number generators - pseudo random coins show more heads than tails. To our surprise, both papers receive considerable public attention.
Computational Complexity and Statistical Mechanics
 A fascinating class of complex systems are combinatorial optimization or
search problems that are classified “hard” by the
theory of computational
complexity. This theory classifies problems according to the
resources (time, memory) needed to solve them on a computer. The standard
classification is based on the worst case scenario, but typical instances
from a random ensemble of “hard” problems are often surprisingly
easy to solve. A theory of
average case complexity is far less
developped than the classical worst case theory, however.
This is
where
statistical mechanics of disordered systems enters the
stage. Developped as a tool to analyze random systems with
a large number of variables, it can be used to investigate the
typical hardness of random optimization and search problems.
A fascinating class of complex systems are combinatorial optimization or
search problems that are classified “hard” by the
theory of computational
complexity. This theory classifies problems according to the
resources (time, memory) needed to solve them on a computer. The standard
classification is based on the worst case scenario, but typical instances
from a random ensemble of “hard” problems are often surprisingly
easy to solve. A theory of
average case complexity is far less
developped than the classical worst case theory, however.
This is
where
statistical mechanics of disordered systems enters the
stage. Developped as a tool to analyze random systems with
a large number of variables, it can be used to investigate the
typical hardness of random optimization and search problems.
A nice account of this interdisciplinary and highly active field of research
has been given by
Marc Mézard in Science 301, 1685 (2003), also
available online.
My contributions
to the field concentrate on the
number partitioning problem,
and recently on the
satisfiability problem.
Low Autocorrelated Binary Sequences
 Binary sequences of +1 and -1 with low autocorrelations have many applications
in communication engineering. Their construction has a long
tradition in engineering and in mathematics. Finding binary sequences with
minimum autocorrelations is a very hard mathematical problem.
In 1987 J. Bernasconi
introduced an Ising spin model that reformulates the problem in
the framework of statistical
mechanics.
Binary sequences of +1 and -1 with low autocorrelations have many applications
in communication engineering. Their construction has a long
tradition in engineering and in mathematics. Finding binary sequences with
minimum autocorrelations is a very hard mathematical problem.
In 1987 J. Bernasconi
introduced an Ising spin model that reformulates the problem in
the framework of statistical
mechanics.
The Bernasconi model is completely deterministic in a sense that there is no explicit or quenched disorder like in spin-glasses. The energy of a configuration is the sum of the square of all correlation coefficients of the spin sequence. The ground states of the Bernasconi model are low autocorrelation binary sequences. As such, the ground states are by definition highly disordered, despite the absence of any explicit disorder. This self-induced disorder resembles the situation in real glasses. In fact, the Bernasconi model exhibits features of a glass transition like a jump in the specific heat and slow dynamics and ageing.
The link to physics has not solved the problem of constructing binary sequences with minimal autocorrelations, however. Exhaustive enumeration of all 2N sequences of length N still is the only means to get true ground states of the Bernasconi model. A clever branch and bound algorithm, running several days on our 160-CPU Beowulf cluster solved the problem up to N=60, which still marks the world record.
For the Bernasconi model with periodic boundary conditions more can be done.
The tight connection between the
correlations of periodic binary sequences and mathematical objects called
cyclic difference sets
can be exploited to get some exact
results on the ground states.
© by Stephan Mertens (Datenschutzerklärung)
![]()
![]()
![]()
Home |
Research |
Publications |
Teaching |
Smorgasbord
![]()
updated on Friday, August 25th 2017, 02:06:34 CET;
