Grain Growth: Monte Carlo Simulation & Theory

Statistical Mean-Field Theory

Two dimensions:
At first we consider the simplified case of two-dimensional grain growth. It is known that normal grain growth is a result of an interaction between the topological problem of space filling and the surface tension equilibrium. For a better understanding of this interaction soap foams have been investigated as an analogue to grain growth in polycrystalline materials for the last decades yielding important results, which have been transmitted to the phenomenon of grain growth. The topic of soap foam evolution has been described first in the early 1950s by C.S. Smith (1952) and is still today of large interest for scientists [Szeto and Tam (1995); Ruskin and Feng (2002)].

Also in 1952 J. von Neumann (1952) discovered that the 2D growth of soap froth depends only on the number of sides. Later in 1956 W.W. Mullins (1956, 1988) found that in analogue to von Neumann’s results the rate of area loss or gain of a given grain depends only on the number of its sides.

Therefore, Mullins (1956) considered the area A of a single grain, which is enclosed by a plane grain boundary with length U, in two dimensions. His investigations resulted in a growth law, which relates the growth rate of all grains to the number of their sides s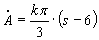

.
This equation is today widely known as the von Neumann-Mullins topological law.

Theis leads to the conclusion that if all grains of an ensemble have six faces the grain structure is in a metastable equilibrium and would not change [Smith (1952)]. Otherwise grain growth occurs. It is important to mention here that a complete equilibrium state is impossible because the grain boundaries are crystallographic defects. For further information regarding an explanation from a pure geometrical point of view please see [Zöllner (2006)].

Three dimensions:
The existence of the ‘(s - 6)-rule’ in two dimensions suggests that there might be an analogue rule also in three dimensions. But in the case of 3D grain growth there is no equivalent equation for the rate of change of the volume of an individual grain with s faces. The difficulty in deriving such a relation is that the velocity of curved grain boundaries is proportional to the mean curvature of their interfaces, whereas the volume changing is related to the Gaussian curvature. Nevertheless since the publications of von Neumann (1952) and Mullins (1956) a generalization for three-dimensional grain growth has been searched.
An answer to this question had partly already been given in 1887 by Lord Kelvin [Lord Kelvin (1887); Weaire (1996)]. He described a possibility to fill the 3D space completely with objects of the same type and size, leading to a regular and symmetric partition of the 3D space. These so called tetrakaidecahedron have each 14 faces (eight hexagonal and six quadratic faces), which are slightly curved. This is mentioned here, because due to the slight curvature grain growth will always occur in such 3D structures and they are therefore not in a metastable equilibrium.

Mullins himself estimated in 1989 the geometrical rate constant in idealized three dimensional grain growth [Mullins (1989)] yielding an average relation between the growth rate of volume of the grains and their number of faces.

Years later Hilgenfeldt et al. (2001) claimed to have found an accurate von Neumann’s law for three dimensional foams. Their derivation is based on a theorem by Minkowski (1903) yielding an explicit analytical von Neumann’s law in 3D, which is in very good agreement with simulations and experiments.

Finally Glicksman (2005) applied integral geometry and topology to the problem of space-filling in irregular network structures such as liquid and amorphous metals, polycrystals, and foams. His theory is based on representing cells in irregular polyhedral networks, so called ‘average N-hedra’, where N equals the number of faces between contacting neighbours. These average N-hedra satisfy, at their edges and vertices, the network’s angular averages for triple lines and quadra junctions, as dictated by the topology. Glicksman showed then that the growth law for average N-hedra may be written in the form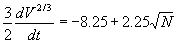

.

However, the conditional stability for six-sided cells in two-dimensional networks does not occur in three-dimensional networks. Instead, the population of N-hedra is divided into shrinking polyhedra for 3 < N < 13, and growing polyhedra for N larger than 14.

In order to study the phenomenon of grain growth more closely Burke and Turnbull (1952) developed already in 1952 one of the first physically motivated grain growth models. They assumed that the migration of grain boundaries happens by transport of matter under a pressure due to the curved surface of the grains, where the grain boundaries always migrate toward their centre of curvature. That is why this kinetics is also called curvature driven kinetics. It reduces the total inner interface, which leads to a minimization of the total interface energy. They showed that the change of the average grain size is given by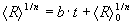

.

In general curvature driven normal grain growth is essentially characterized by the following two properties:

The average grain size < R > of an ensemble of grains of a polycrystalline solid increases with time t according to the growth law [Hillert (1965); Louat (1974)]
.
In all three fields of investigation of grain growth - theory [Burke and Turnbull (1952); Mullins and Vinals (1989)], computer simulations [Grest et al. (1988); Weaire and Kermode (1984); Zöllner (2006)] and experiments [Glazier et al. (1987); Weaire and Kermode (1983)] - the grain growth factor n is supposed to have a value of n = 0.5.
The underlying coarsening process of the grain structure develops towards a quasi-stationary state that exhibits statistical self-similarity (see [Burke (1949); Mullins (1986)]). The latter means that the grain size distribution function F(R,t) in the quasi-stationary state is characterized by the scaling form
,
where f(x) is the scaled time-invariant size distribution function, which only depends on the relative grain size x := R/< R >. From volume conservation the time-dependent factor follows as g(t) = N/< R >.

In the statistical mean-field theory of grain growth [Atkinson (1988); Thompson (2001)] it is assumed that the above grain size distribution function (GSDF) obeys the Fokker-Planck-equation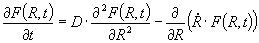

.
The term on the left-hand side calculates the temporal change of the grain size distribution function. The first term on the right-hand side is a diffusion term with D as a diffusion constant corresponding to stochastic processes in the size space of grains. The second term on the right-hand side represents the drift term corresponding to an average growth law.

Louat (1974) assumed that the diffusion term is the dominating one considering grain growth as a purely random diffusion-like process yielding the size distribution function as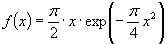

.
This distribution function has no cut-off, but a tail yielding a very broad size distribution.

On the other hand Hillert (1965) assumed that the drift velocity dominates normal grain growth and that this driving force yields the elimination of the grain boundary area. Therefore, the first term on the right-hand side is ignored and set equal to 0 yielding an equation This equation that is also called continuity equation in size space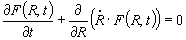

.
In his pioneering work on grain growth Hillert (1965) used concepts from the Lifshitz-Slyozov-Wagner theory [Lifshitz and Slyozov (1961); Wagner (1961)], who introduced in 1961 the growth law for Ostwald-Ripening. By integration of the continuity equation Hillert obtained his well-known scaled grain size distribution function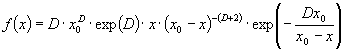

where D is the dimension of the considered system (either D = 2 for two-dimensional grain growth or D = 3 for three-dimensional grain growth). However, Hillert’s grain size distribution function has never been observed, neither experimentally, nor by computer simulations.

Note:
The diffusion term in the Fokker-Planck-equation is connected with stochastic processes that arise from abrupt changes caused by grain switching events, in which the number of faces or sides of a grain changes discontinuously. Mullins (1998) has pointed out that the time scale of such process does not contribute to the Fokker-Planck-equation. That means that the diffusion term virtually vanishes and the Fokker-Planck-equation reduces to the continuity equation in size space.
Streitenberger (1998), however, has shown that Louat’s size distribution function represents also a solution of the continuity equation, namely in the frame of a generalised Lifshitz-Slyozov-Wagner (LSW) theory [Lifshitz and Slyozov (1961); Wagner (1961)] for an infinite cut-off.

However, by means of computer simulations of two-dimensional grain growth [Marthinsen et al. (1996); Brandt et al. (1998); Nordbakke et al. (2002)] the existence of grain size correlations between neighbouring grains has been revealed that is not represented by Hillert’s linear growth law. Stimulated by such computer simulations many attempts have been made to improve Hillert’s theory. The adequate consideration of the observed spatial size correlations in the effective growth law yielded, in combination with the LSW-method, analytical grain size distribution functions for two-dimensional grain growth [Streitenberger (1998, 2001); Rios and Lücke (2001); Nordbakke et al. (2004)] and lately also for three-dimensional grain growth [Zöllner and Streitenberger (2006); Streitenberger and Zöllner (2006, 2007); Zöllner (2006)], which were in good agreement with the grain size distribution functions of the simulations.

Statistical mean-field theory:
In order gain an analytic grain size distribution from the continuity equation in size space we need a statement about the growth law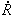

, which is related to the volume change rate by

.
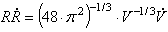For further details compare also Chapter Volumetric Rate of Change, where we have shown that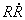

can be approximated as a quadratic function in x,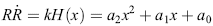

.

An analytical mean-field theory corresponding to the quadratic growth law for 3D grain growth has been given in [Streitenberger (1998); Streitenberger (2001); Zöllner and Streitenberger (2006); Zöllner (2006)]. This theory is based on the analytical approximation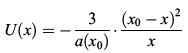

,
where the relation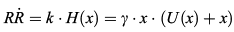

holds with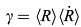

.

Here x₀ is a free parameter fixing the double root of U(x) in correspondence with the Lifshitz-Slyozov stability conditions.
Inserting this approximation in the continuity equation yields the following normalized self-similar grain size distribution function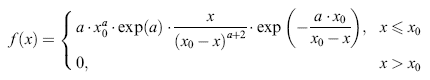

with x₀ as an upper cut-off parameter calculated by the implicit equation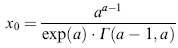

.

This derivation is part of a more general description that can be found in [Streitenberger and Zöllner (2006); Zöllner (2006)].

[Smith (1952)]	C.S. Smith. Seminar Report (Cleveland, Ohio: American Society for Metals). Metal Interfaces, page 65, 1952.
[Szeto and Tam (1995)]	K.Y. Szeto and W.Y. Tam. Lewis’ law versus Feltham’s law in soap froth. Physics A: Statistical and Theoretical Physics, 221:256, 1995.
[Ruskin and Feng (2002)]	H.J. Ruskin and Y. Feng. Constrained geometries in soap froth dynamics. Physics A: Statistical Mechanics and its Applications, 314:362, 2002.
[von Neumann (1952)]	J. von Neumann. Seminar Report (Cleveland, Ohio: American Society for Metals). Metal Interfaces, page 108, 1952.
[Mullins (1956)]	W.W. Mullins. Two-dimensional motion of idealized grain boundaries. Journal of Applied Physics, 27:900, 1956.
[Mullins (1988)]	W.W. Mullins. On idealized two dimensional grain growth. Scripta Metallurgica, 22:1441, 1988.
[Lord Kelvin (1887)]	Lord Kelvin. On the division of space with minimum partitional area. Philosophical Magazine, 24:503, 1887.
[Weaire (1996)]	D. Weaire. The Kelvin Problem, Foam Structures of Minimal Surface Area. Taylor & Francis, 1996.
[Mullins (1989)]	W.W. Mullins. Estimation of the geometrical rate constant in idealized three dimensional grain growth. Acta Metallurgica, 37:2979, 1989.
[Hilgenfeldt et al. (2001)]	S. Hilgenfeldt, A.M. Kraynik, S.A. Koehler, and H.A. Stone. An accurate von Neumann’s law for three-dimensional foams. Rhysical Review Letters, 86:2685, 2001.
[Minkowski (1903)]	H. Minkowski. Volumen and Oberfläche. Math. Ann., 57:447, 1903.
[Glicksman (2005)]	M.E. Glicksman. Analysis of 3-d network structures. Philosophical Magazine, 85:3, 2005.
[Burke and Turnbull (1952)]	J.E. Burke and D. Turnbull. Recrystallization and grain growth. Progress in Metal Physics, 3:220, 1952.
[Hillert (1965)]	M. Hillert. On the theory of normal and abnormal grain growth. Acta Metallurgica, 13:227, 1965.
[Louat (1974)]	N.P. Louat. On the theory of normal grain growth. Acta Metallurgica, 22:721, 1974.
[Mullins and Vinals (1989)]	W.W. Mullins and J. Vinals. Self-similarity and growth kinetics driven by surface free energy reduction. Acta Metallurgica, 37:991, 1989.
[Grest et al. (1988)]	G.S. Grest, M.P. Anderson, and D.J. Srolovitz. Domain-growth kinetics for the Q-state Potts model in two and three dimensions. Physical Review B, 38:4752, 1988.
[Weaire and Kermode (1984)]	D. Weaire and J.P. Kermode. Computer simulation of a two-dimensional soap froth II. Analysis of results. Philosophical Magazine B, 50:379, 1984.
[Glazier et al. (1987)]	J.A. Glazier, S.P. Gross, and J. Stavans. Dynamics of two-dimensional soap froths. Physical Review A, 36:306, 1987.
[Weaire and Kermode (1983)]	D. Weaire and J.P. Kermode. The evolution of the structure of a two-dimensional soap froth. Philosophical Magazine B, 47:L29, 1983.
[Burke (1949)]	J.E. Burke. Some factors affecting the rate of grain growth in metals. Transactions of the Metallurgical Society of AIME, 180:73, 1949.
[Mullins (1986)]	W.W. Mullins. The statistical self-similarity hypothesis in grain growth and particle coarsening. Journal of Applied Physics, 59:1341, 1986.
[Atkinson (1988)]	H.V. Atkinson. Theories of normal grain growth in pure single phase systems. Acta Metallurgica, 36:469, 1988.
[Thompson (2001)]	C.V. Thompson. Grain growth and evolution of other cellular structures. Solid State Physics, 55:269, 2001.
[Lifshitz and Slyozov (1961)]	I.M. Lifshitz and V.V. Slyozov. The kinetics of precipitation from supersaturated solid solutions. Journal of Physics and Chemistry of Solids, 19:35, 1961.
[Wagner (1961)]	C.Wagner. Theorie der Alterung von Niederschlägen durch Umlösen (Ostwald-Reifung). Zeitung für Elektrochemie, 65:581, 1961.
[Mullins (1998)]	W.W. Mullins. Grain growth of uniform boundaries with scaling. Acta Materialia, 46:6219, 1998.
[Marthinsen et al. (1996)]	K. Marthinsen, O. Hunderi, and N. Ryum. The influence of spatial grain size correlation and topology on normal grain growth in two dimensions. Acta Materialia, 44:1681, 1996.
[Brandt et al. (1998)]	R. Brandt, J. Svoboda, and K. Lücke. Simulations of grain growth in 2d by the statistical theory and by a direct method. In H. Weiland et al., editors, Grain growth in polycrystalline materials III, page 131, Warrendale (PA), 1998. TMS.
[Nordbakke et al. (2002)]	M.W. Nordbakke, N. Ryum, and O. Hunderi. Invariant distributions and stationary correlation functions of simulated grain growth processes. Acta Materialia, 50:3661, 2002.
[Rios and Lücke (2001)]	P.R. Rios and K. Lücke. Comparison of statistical analytical theories of grain growth. Scripta Materialia, 44:2471, 2001.
[Nordbakke et al. (2004)]	M.W. Nordbakke, N. Ryum, and O. Hunderi. Curvilinear polygons, finite circle packings, and normal grain growth. Materials Science and Engineering: A, 385:229, 2004.

[Streitenberger (1998)]	P. Streitenberger. Generalized Lifshitz-Slyozov theory of grain and particle coarsening for arbitrary cut-off parameter. Scripta Materialia, 39:1719, 1998.
[Streitenberger (2001)]	P. Streitenberger. Analytical model of grain growth based on a generalized ls stability argument and topological relationships. In G. Gottstein and D.A. Molodov, editors, Recrystallization and grain growth, 257, Berlin, 2001. Springer.
[Zöllner and Streitenberger (2006)]	D. Zöllner and P. Streitenberger. Three-dimensional normal grain growth: Monte Carlo Potts model simulation and analytical mean field theory. Scripta Materialia, 54:1697, 2006.
[Streitenberger and Zöllner (2006)]	P. Streitenberger and D. Zöllner. Effective growth law from three-dimensional grain growth simulations and new analytical grain size distribution. Scripta Materialia, 55:461, 2006.
[Streitenberger and Zöllner (2007)]	P. Streitenberger and D. Zöllner. Topology based growth law and new analytical grain size distribution function of 3D grain growth. Materials Science Forum, Vols.558-559, 1183, 2007.

[Zöllner (2006)]	D. Zöllner. Monte Carlo Potts Model Simulation and Statistical Mean-Field Theory of Normal Grain Growth. Shaker-Verlag, Aachen, 2006.

Datenschutzerklärung der Otto-von-Guericke-Universität Magdeburg nach DSGVO
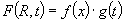